在数字时代中,数字化文档的认证性、完整性和不可否认性,是实现信息化安全的基本要求。数字签名则是满足上述要求的主要方式之一,亦是现代密码学的研究内容之一。
数字签名有哪些形式?基于密码学的数字签名优势几何?有哪些常用的数字签名实现方案?使用过程中又潜藏何等风险?我们将先从理解概念为始,再为大家逐步深入介绍。
区块链百科No.34:基于椭圆曲线签名方案
随着计算机信息处理能力的不断提高,对密钥长度的要求也越来越高,这个问题对于存储能力受限的系统来说显得尤为突出。
椭圆曲线密码体制(ECC)的提出改变了这种状况,它可以用更短的密钥提供与其他体制相当的或者更高级的安全,并已成为迄今被实践证明安全、有效、应用较广的3种公钥密码体制之一。本文将继续为大家介绍基于椭圆曲线的数字签名方案。
椭圆曲线
椭圆曲线在代数学和几何学上,已被广范研究了150年之久,有坚实的理论基础。
所谓椭圆曲线是指维尔斯特斯拉(Weierstrass)方程:

所确定的平面曲线,其中a、b、c、d、e属于域F,其可以是有理数域Q、复数域C,还可以是有限域GF(p)。
椭圆曲线是其上所有点(x、y)的集合,外加一个无穷远点O(定义椭圆曲线上一个特殊的点,记为O,它为仿射平面无穷远的点,称为无穷远点。在xOy平面上,可以看做平行于y轴的所有直线的集合的一种抽象)。
密码学中普遍采用的是有限域上的椭圆曲线,它是指椭圆曲线方程定义式中,所有的系数都是在某一有限域GF(p)中的元素。它最简单的公式为:

该椭圆曲线上只有有限个离散点,设为N,则N称为椭圆曲线的阶为N。N越大,安全性越高。基于此,椭圆曲线的图示可以表示如下:

当然,基于不同变量值,椭圆曲线还有其他的表示形式:

当我们仔细观察这些曲线时,能发现一些有趣特性:(1)对称性,即曲线上的任何一点都可以在x轴上反射,并保持曲线不变;(2)任何非垂直直线与曲线的交点至多有三个。
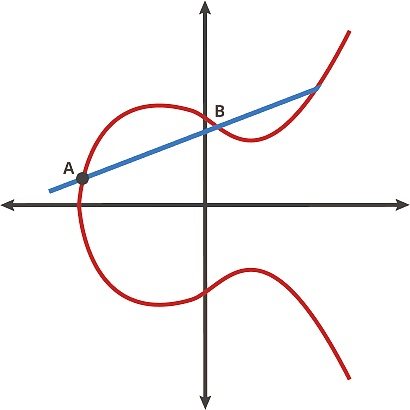
我们可以把这条曲线想象成一场桌球游戏。在曲线上取任意两点并通过它们画一条直线,它将与曲线相交于另一个位置。在这个桌球游戏中,你在A点拿一个球,把它射向B点,当它击中曲线时,球要么直接向上反弹(如果它在x轴以下),要么直接向下反弹(如果它在x轴以上)到曲线的另一边。我们可以把球看做在两个点间移动,曲线上的任意两点碰撞可得到一个新的点。
A·B = C
或者可以用某一个点自身不断碰撞出新的点。
A·A = B
A·B = C
A·C = D
……
在这个过程中,一个初始点经由n次运算会得到最后到达的点,当你只知道这两个点的值,要找出n是很难的。

这就像一个人在房间里随机玩一段时间桌球游戏,对他而言,按照上面描述的规则一遍又一遍地击球是很容易的。但如果有人走进房间,球刚好结束到达一个点,即使他知道所有的游戏规则,以及球从哪个点开始,也不能确定球到达此处所被击中的次数。容易正向计算,难以反向计算,这也是陷门函数的基础。
基于椭圆曲线的签名方案
1985年,Koblitz和Miller将椭圆曲线引入密码学,提出了基于有限域GF(p)的椭圆曲线上的点集构成群,在这个群上定义离散对数难题并构造出基于其的一类公钥密码体制,即基于椭圆曲线的离散密码体制,其安全性基于椭圆曲线上离散对数问题的难解性。
我们以基于椭圆曲线的ECDSA数字签名实现方案为例,阐述其具体的实现过程。
密钥生成算法
假设GF(p)为有限域,E是有限域GF(p)上的椭圆曲线。选择E上一点G∈E,G的阶为满足安全要求的素数n,即nG=O(O为无穷远点)。
选择一个随机数d,d∈[1,n-1],计算Q,使得Q=dG。那么公钥为(n,Q),私钥为d。
签名算法
假设待签名的消息为m,经过如下计算过程,签名者对消息m的数字签名为(r,s)。

验证算法
签名接收者B对消息m签名(r,s)的验证过程如下:

判断r和r1的关系,如果相等,则签名有效;否则,签名无效。
除了上述介绍ECDSA方案之外,基于椭圆的数字签名方案还有很多,而类似DSA的其他方案例如Schnorr、EIGamal等方案也都被移植到椭圆曲线有限群上。
椭圆曲线签名方案解析
从上述介绍可知,数字签名的安全性依赖于基于椭圆曲线的有限群上的离散对数难题。
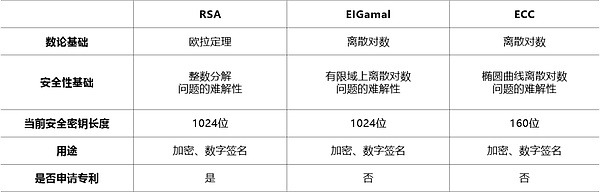
与前章所述RSA数字签名和基于有限域离散对数的数字签名相比,基于椭圆曲线的数字签名方案具有如下特点:在相同的安全强度条件下,签名长度短,密钥存储空间小,适用于存储空间有限,带宽受限、要求高速实现的场合。
此外,椭圆曲线资源丰富,同一有限域上存在着大量不同的椭圆曲线,这也为安全性增加了额外的保障。
正是由于椭圆曲线具有丰富的群结构和多选择性,并可以在保持和RSA、EIGamal体制同样安全性的前提下大大缩短密钥长度,因而有着更为广阔的应用场景。
 世纪金融网
世纪金融网






